Teaching for Mastery
Discover what teaching for mastery means and how to get involved
What is Teaching for Mastery
Mastering maths means pupils acquiring a deep, long-term, secure and adaptable understanding of the subject.
The phrase ‘teaching for mastery’ describes the elements of classroom practice and school organisation that combine to give pupils the best chances of mastering maths.
Achieving mastery means acquiring a solid enough understanding of the maths that’s been taught to enable pupils to move on to more advanced material.
Five big ideas in Teaching for Mastery
A central component in the NCETM/Maths Hubs programmes to develop Mastery Specialists has been discussion of Five Big Ideas, drawn from research evidence, underpinning teaching for mastery. The diagram below is used to help bind these ideas together.
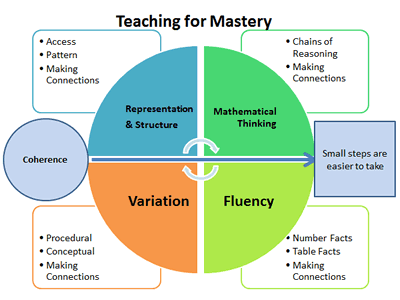
Coherence
Lessons are broken down into small connected steps that gradually unfold the concept, providing access for all children and leading to a generalisation of the concept and the ability to apply the concept to a range of contexts.
Representation and Structure
Representations used in lessons expose the mathematical structure being taught, the aim being that students can do the maths without recourse to the representation
Mathematical Thinking
If taught ideas are to be understood deeply, they must not merely be passively received but must be worked on by the student: thought about, reasoned with and discussed with others.
Fluency
Quick and efficient recall of facts and procedures and the flexibility to move between different contexts and representations of mathematics
Variation
Variation is twofold. It is firstly about how the teacher represents the concept being taught, often in more than one way, to draw attention to critical aspects, and to develop deep and holistic understanding. It is also about the sequencing of the episodes, activities and exercises used within a lesson and follow up practice, paying attention to what is kept the same and what changes, to connect the mathematics and draw attention to mathematical relationships and structure.



